728x90
반응형
https://en.wikipedia.org/wiki/Merge_sort
Merge sort - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Divide and conquer-based sorting algorithm In computer science, merge sort (also commonly spelled as mergesort) is an efficient, general-purpose, and comparison-based sorting algorithm
en.wikipedia.org
합병 또는 병합 정렬은 분할 정복 알고리즘 중 하나이다.
자세한 내용은 위의 위키피디아의 정의를 참고하면 될 것 같다.
n(= 8)개의 데이터가 들어왔다고 가정한다.
* Step 1. 리스트의 길이가 1이 될때 까지 분할한다.

* Step 2. 분할 될 리스트끼리 오름차순으로 정렬한 후 합병한다.
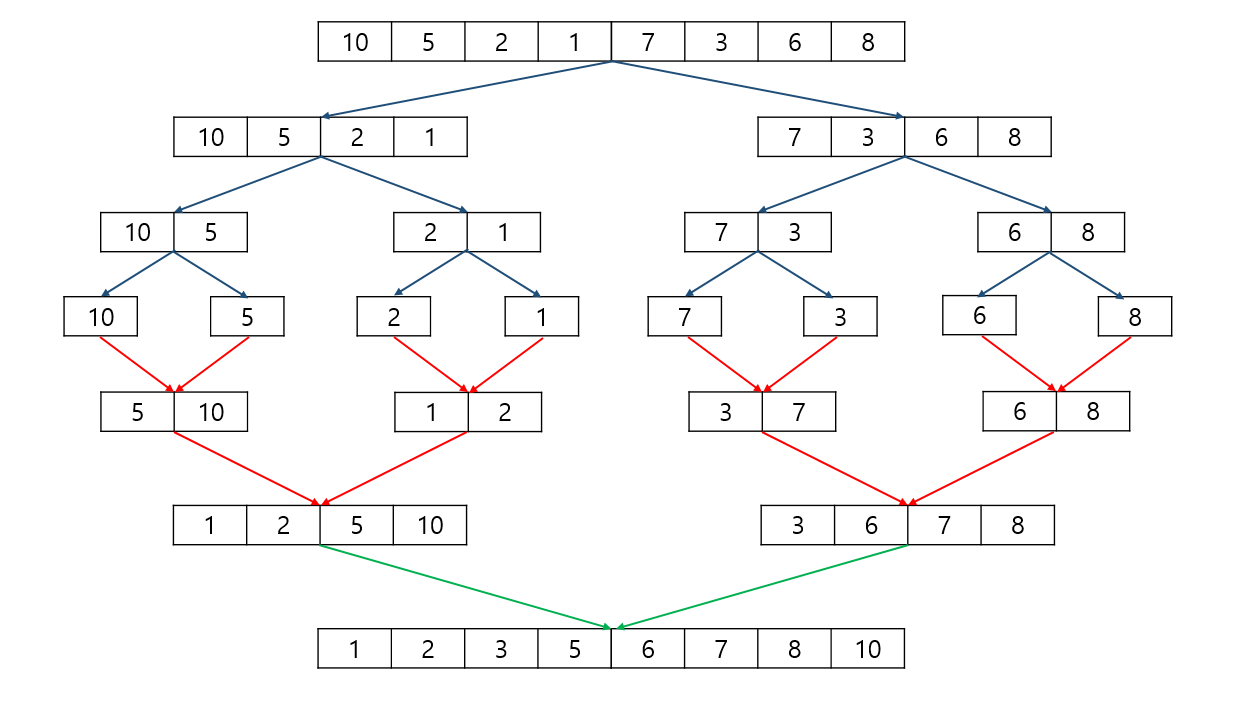
위의 예제를 자세히 살펴보면,
1. 배열 길이 1
- 10과 5를 비교하여 더 작은 값을 새로운 배열에 삽입한 뒤, 더 큰 값을 그 뒤에 삽입한다.
(2와 1, 7과 3, 6과 8도 동일)
2. 배열 길이 2
- arr_1[5,10]과 arr_2[1, 2] 를 정렬하고자 할때는, 각 배열의 첫번째 방끼리 비교하여 더 작은 값을 새로운 배열에 삽입한다. 또한, 삽입된 값은 기존의 배열에서 삭제한다.
1) 5 > 1 => new_arr[1], ( arr_1[5, 10] arr_2[2] )
2) 5 > 2 => new_arr[1, 2], ( arr_1[5, 10] arr_2[] )
3) 비교할 배열의 값이 없기 때문에, new_arr에 남은 배열을 삽입
=> new_arr[1, 2, 5, 10]
3. 배열 길이 4
- arr_1[1, 2, 5, 10]과 arr_2[3, 6, 7, 8]
1) 1 < 3 => new_arr[1], ( arr_1[2, 5, 10] arr_2[3, 6, 7, 8] )
2) 2 < 3 => new_arr[1, 2], ( arr_1[5, 10] arr_2[3, 6, 7, 8] )
3) 5 > 3 => new_arr[1, 2, 3] ( arr_1[5, 10] arr_2[6, 7, 8] )
4) 5 < 6 => new_arr[1, 2, 3, 5] ( arr_1[10] arr_2[6, 7, 8] )
5) 10 > 6 => new_arr[1, 2, 3, 5, 6] ( arr_1[10] arr_2[7, 8] )
6) 10 > 7 => new_arr[1, 2, 3, 5, 6, 7] ( arr_1[10] arr_2[8] )
7) 10 > 8 => new_arr[1, 2, 3, 5, 6, 7, 8] ( arr_1[10] arr_2[] )
8) 10 => new_arr[1, 2, 3, 5, 6, 7, 8, 10] ( arr_1[] arr_2[] )
합병 정렬은 n 개의 데이터에 log n 단계를 수행하므로 O(n log n)의 수행 시간이 필요하다.
# merge_sort
def merge_sort(original_list):
if len(original_list) < 2 :
return original_list
mid = len(original_list) // 2
low_arr = merge_sort(original_list[:mid])
high_arr = merge_sort(original_list[mid:])
merged_arr = []
l = h = 0
while l < len(low_arr) and h < len(high_arr):
if low_arr[l] < high_arr[h]:
merged_arr.append(low_arr[l])
l += 1
else:
merged_arr.append(high_arr[h])
h += 1
merged_arr += low_arr[l:]
merged_arr += high_arr[h:]
return merged_arr
original_list = [3, 7, 4, 8, 6, 2, 1, 5 ]
print("origin_list", original_list)
final_list = merge_sort(original_list)
print("final_list ", final_list)'Basic IT Knowledge' 카테고리의 다른 글
| Odyssey 스킨에 글 수정, 삭제 버튼 넣기 - 공부하는 도비 (0) | 2022.10.14 |
|---|---|
| Free 3D Model Download Site - 공부하는 도비 (0) | 2022.09.16 |
| Bubble Sort - 공부하는 도비 (0) | 2022.08.06 |
| Slideshare에서 PPT(files) 무료로 다운 받기 - 공부하는 도비 (0) | 2022.07.22 |
| Latex Algorithm - 공부하는 도비 (0) | 2022.03.22 |